在醫學研究中,常需要一群病人的存活狀態。而其中,Cox proportional hazards model就特別常使用到。它的長處是可以對於不同的資料型態包含類別變相與連續變相一起做多變數校正,去找出統計學上影響存活的因子有哪些。就如同多數檢定,這個檢定也有自己的assumption,也就是proportional hazards assumption(簡稱PH assumption)。實務上要如何執行呢?
預先準備好要分析的資料,包含時存活時間函數,事件發生紀錄與欲探討的變數。
在SPSS中,選擇Analyze - Survival - Kaplan-Meirer...
在Time放入時間函數
在Status放入事件發生紀錄
在Factor放入要分析的變數
接著按下右邊小按鈕"Options..."
預先準備好要分析的資料,包含時存活時間函數,事件發生紀錄與欲探討的變數。
在SPSS中,選擇Analyze - Survival - Kaplan-Meirer...
在Time放入時間函數
在Status放入事件發生紀錄
在Factor放入要分析的變數
接著按下右邊小按鈕"Options..."
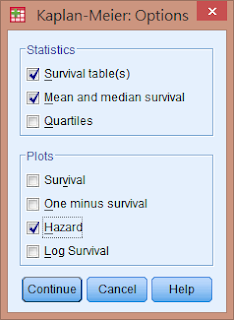
這一步,多數人用過Plots - Suvival這個功能,也就是很常見的Kaplan-Meier存活曲線。但今天介紹的重點是檢驗proportional hazards assumption所以我們要把Plots中第三個"Hazard"勾選。接著按Continue確認。回到主畫面就可以按"OK"
接著,就會進行運算,運算結果最後一項就會是Hazrard圖。
判定的方法呢,其實很容易,就是檢查分開的兩條線有沒有交叉。
如果沒有交叉,符合proportional hazards assumption,而若交叉了,就沒有符合proportional hazards assumption了。
範例判定可以看看參考資料,是個英文的教學檔,可以在圖片中看到未交叉與交叉的範例。
參考資料





Easy "water hack" burns 2 lbs OVERNIGHT
回覆刪除At least 160 000 women and men are losing weight with a simple and secret "water hack" to lose 1-2 lbs each and every night while they sleep.
It's painless and it works on anybody.
This is how to do it yourself:
1) Grab a drinking glass and fill it up with water half full
2) Then use this weight losing HACK
you'll become 1-2 lbs thinner as soon as tomorrow!